动态规划之0-1背包问题

最近在学习动态规划（Dynamic programming），其经典问题之一就是 0-1 背包问题。

题目描述为：有一个背包，其容量为 C（capacity）。现在有 n 种不同的物品，编号为 0…n-1，其中每个物品的重量为 w(i)，价值为 v(i)。问可以向这个背包中放入哪些物品，使得在不超过背包容量的前提下，物品的价值最大。

函数签名为：int knapsack01(int[] w, int[] v, int C)

下面先说「自顶向下」的记忆化搜索递归解法

递归解法的函数签名为：int tryBestValue(int[] w, int[] v, int index, int c)。

对于一个 dp 问题，我们要先明确「状态」和「选择」。状态是，「背包的容量」和「可选的物品」。就是递归参数 index 和 c。选择是，放入背包，或者不放入背包。

对于选择可能好理解，一个物品要么放要么不放。对状态的简单理解就是，如果你用递归的方式求解，递归传入的参数就是状态。这里要排除那些不会变的参数，比如 w 和 v，因为每个物品的重量和价值是不变的，其状态是不需要转移的。

对于背包问题，递归函数可以定义为 F(n, C)，考虑将 n 个物品放入放进容量为 C 的背包，使得价值最大。注意用的是考虑，说明当前的递归函数的解可能并不是最优解。

状态转移也好理解。当调用到递归函数时，给递归函数传入的参数是要变的。这一变，状态就转移了，将当前状态转移为下一个状态。

那么状态转移方程就是：

其实进行到这里，如果不考虑时间、空间消耗的话，已经可以求出最优解了。

但是该问题是有重叠子问题的，那么我们就要用 memo 来进行记忆化搜索，以排除递归过程中的重复计算。因为状态有两个，index 和 c，所以这里的 memo 应该是一个二维数组，行表示背包的容量，列表示物品编号。

完整代码是：

public class Solution {

    private int[][] memo;

    public int knapsack(int[] w, int[] v, int C){
        int n = w.length;
        memo = new int[n][C + 1];

        for (int[] m : memo) {
            Arrays.fill(m, -1);
        }

        return tryBestValue(w, v, n - 1, C);
    }

    // 用 [0...index] 的物品，填充容积为 c 的背包的最大价值
    private int tryBestValue(int[] w, int[] v, int index, int c) {
        // base case，当前背包没容量了，或者背包有容量但是没物品了
        if (c <= 0 || index < 0) {
            return 0;
        }

        // memo[index][c] 的值被更改过，直接返回
        if(memo[index][c] != -1) {
            return memo[index][c];
        }

        // index 不放入背包
        int res = tryBestValue(w, v, index-1, c);
        // 在确保背包剩余容量可以容纳物品 index 的情况下，将index 放入背包。
        if(c >= w[index]) {
            // 求两种选择的最大值
            res = Math.max(res, v[index] + tryBestValue(w, v, index - 1, c - w[index]));
        }

        return memo[index][c] = res;
    }
}

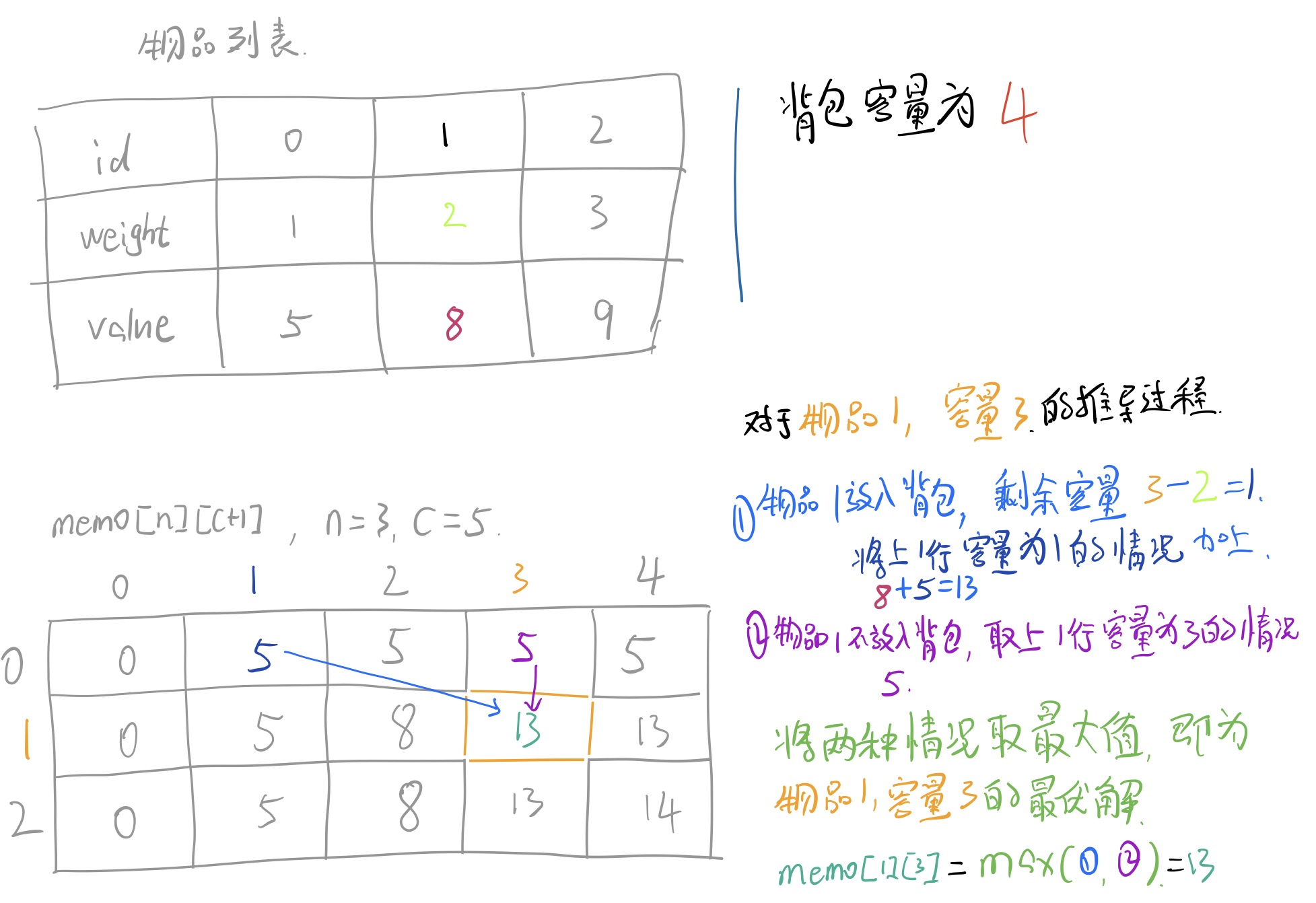
说完「自顶向下」的记忆化搜索解法，接下来再说下「自底向上」的动态规划解法

动态规划需要有最基本的情况，后面的情况可以根据前面的情况来推导。在推导后面的情况时，前面的情况已经是最优解了，不会再变了。

Tip: 建议先画出 dp 数组的结构，并添上一些值。就像上图的 dp 数组。然后根据画出的 dp 数组来推导状态转移方程。不然光用脑袋想太抽象了。

完整代码是：

public class Solution {

    public int knapsack(int[] w, int[] v, int C){
        int n = w.length;
        int[][] dp = new int[n][C + 1];

        // 初始化 memo。初始情况只考虑物品 0
        // 看只给你物品 0 的情况下，背包的每种容量中可以放入的最大价值是多少
        // 也就是初始化 memo 数组的第一行
        for(int j = 0 ; j <= C ; j ++) {
            dp[0][j] = (j >= w[0] ? v[0] : 0);
        }

        for(int i = 1 ; i < n ; i ++) {
            for (int j = 0; j <= C; j++) {
                // 物品 i 不放入背包
                dp[i][j] = dp[i - 1][j];
                if (j >= w[i])
                    // 物品 i 放入背包：v[i] + memo[i - 1][j - w[i]]
                    dp[i][j] = Math.max(dp[i][j], v[i] + dp[i - 1][j - w[i]]);
            }
        }

        return dp[n - 1][C];
    }}

背包问题的变种：

Leetcode 494. 目标和

public int findTargetSumWays(int[] nums, int target) {
    int sum = 0;
    for (int n : nums) sum += n;

    int diff = sum - target;

    if (diff < 0 || diff % 2 != 0) return 0;

    // neg：「加负号的元素」的和
    // 等价于背包总容量就为 neg
    int neg = diff / 2;
    int n = nums.length;
    int[][] dp = new int[n + 1][neg + 1];

    dp[0][0] = 1;

    for (int i = 1; i <= n; i++) {
        int num = nums[i - 1];

        for (int j = 0; j <= neg; j++) {
            // 不将元素 i-1 放入背包
            dp[i][j] = dp[i - 1][j];

            if (j >= num) {
                // 将元素 i-1 放入背包
                dp[i][j] += dp[i - 1][j - num];
            }
        }
    }

    return dp[n][neg];
}