刷题「栈和队列」相关

用栈实现队列（简单）

栈的特点是「先进后出」。队列的特点是「先进先出」。现在要求使用后进先出的栈实现一个先进先出的队列。也就是要保证栈顶的元素始终是队首的元素。

方法一：

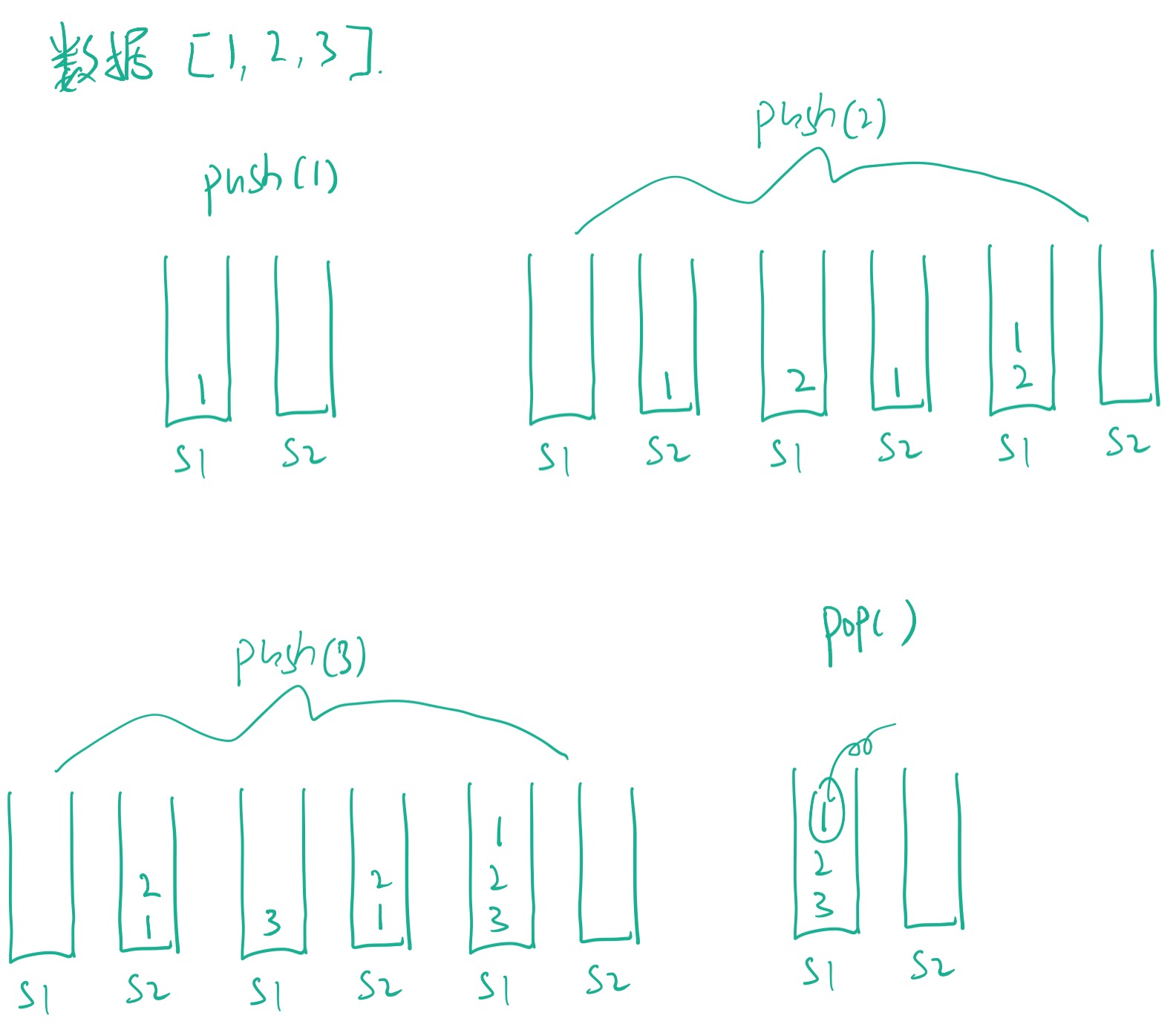
我们可以用两个栈来实现。其中一个栈用来存储数据，我们称为「数据栈」，另外一个栈用来辅助将数据倒序push进第一个栈的，我们称为「辅助栈」。因为，这样可以让数据栈的数据保持新来的数一直在栈顶，这样可以实现「先进先出」。

画图如下：

class MyQueue:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        # 数据栈
        self.stack1 = []
        # 辅助栈
        self.stack2 = []
        # 数据的个数，用来指向栈顶元素
        self.size = 0


    def push(self, x: int) -> None:
        """
        Push element x to the back of queue.
        """
        # 先把数据栈里的数据放到辅助栈
        while self.stack1:
            self.stack2.append(self.stack1.pop())

        # 在数据栈中压入新来的数
        self.stack2.append(x)

        # 再将辅助栈的数据放回数据栈
        while self.stack2:
            self.stack1.append(self.stack2.pop())

        self.size += 1


    def pop(self) -> int:
        """
        Removes the element from in front of queue and returns that element.
        """
        self.size -= 1
        return self.stack1.pop()

    def peek(self) -> int:
        """
        Get the front element.
        """
        if self.stack1 != []:
            return self.stack1[self.size - 1]
        else:
            return None

    def empty(self) -> bool:
        """
        Returns whether the queue is empty.
        """
        return self.stack1 == []

复杂度分析：

时间复杂度：入队O(n)，出队O(1)，取队首元素O(1)，判空O(1)。

空间复杂度：入队O(n)，出队O(1)，取队首元素O(1)，判空O(1)。

方法二：

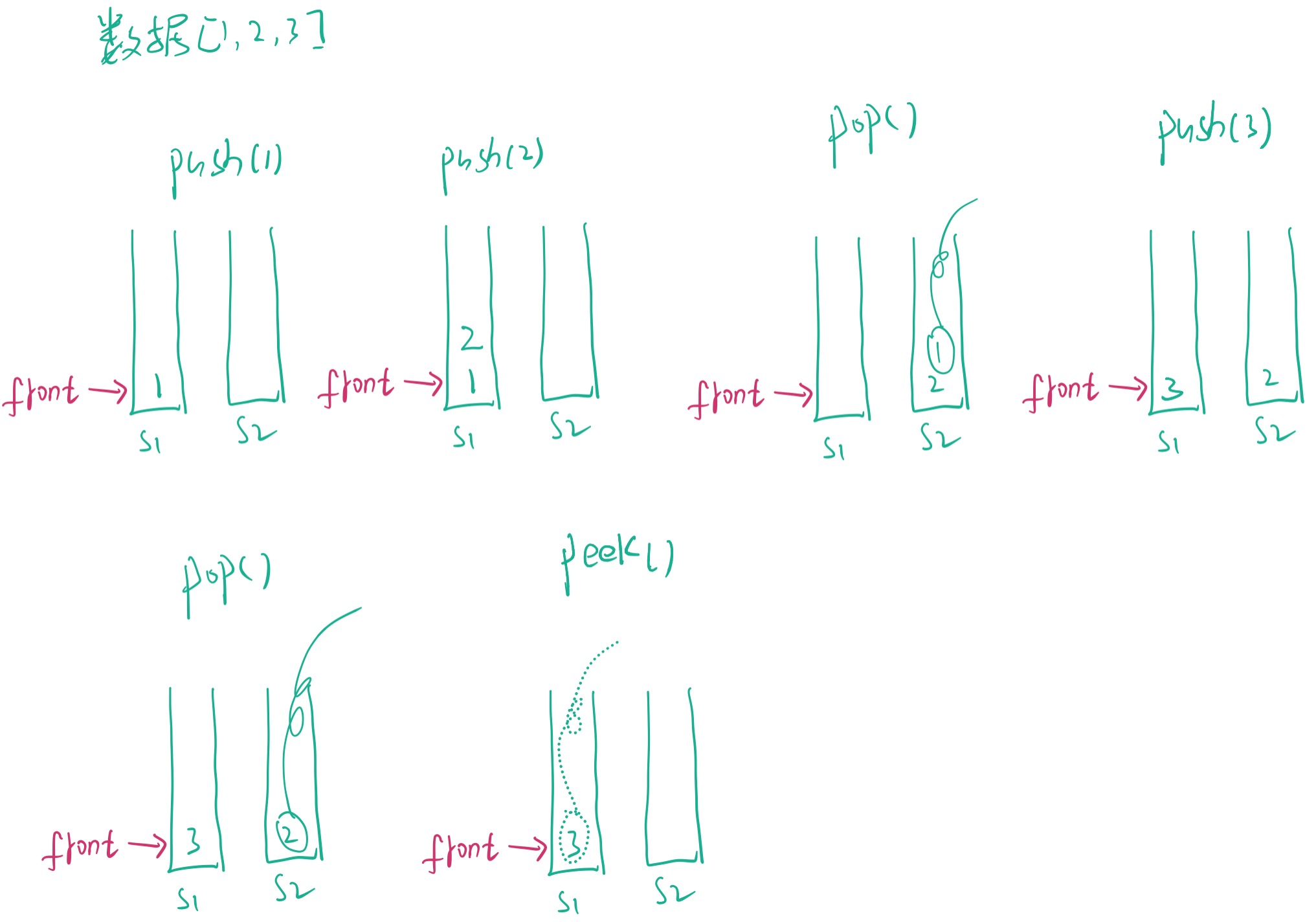
还是使用两个栈，只不过现在两个栈中都存放数据。两个栈的区别是，只有当出栈pop时，才把stack1的数据放到stack2中，然后return stack2.pop()。为了实现peek方法，同时还要维护一个front变量，使其一直指向stack1的栈底元素，因为只是peek一下，所以不用像pop那样将stack1的数据移动到stack2中，这样可在O(1)的复杂度实现peek方法。

画图如下：

class MyQueue:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.stack1 = []
        self.stack2 = []
        self.sizeOfStack2 = 0
        self.front = None


    def push(self, x: int) -> None:
        """
        Push element x to the back of queue.
        """
        # 如果stack1空，则
        if not self.stack1:
            self.front = x
        self.stack1.append(x)


    def pop(self) -> int:
        """
        Removes the element from in front of queue and returns that element.
        """
        if not self.stack2:
            while self.stack1:
                self.stack2.append(self.stack1.pop())
                self.sizeOfStack2 += 1
        self.sizeOfStack2 -= 1
        return self.stack2.pop()


    def peek(self) -> int:
        """
        Get the front element.
        """
        # 如果stack2不为空，就直接返回其栈顶元素
        if self.stack2:
            return self.stack2[self.sizeOfStack2 - 1]
        # 如果为空，因为只是peek一下，所以不用将stack1的数据转移到stack2中，直接返回维护好的front即可。
        else:
            return self.front


    def empty(self) -> bool:
        """
        Returns whether the queue is empty.
        """
        return self.stack1 == [] and self.stack2 == []

复杂度分析：

时间复杂度：入队O(1)，出队均摊复杂度O(1)，取队首元素O(1)，判空O(1)。

空间复杂度：入队O(n)，出队O(1)，取队首元素O(1)，判空O(1)。

---

用队列实现栈（简单）

要用队列来实现栈的特性，就是要保证队首的元素始终是栈顶的元素。

可以用两个队列来实现，一个是数据队列，一个是辅助队列。辅助队列的作用是在将新元素入数据队列前，先将数据队列数据移动到辅助队列，然后数据队列入队新元素，最后将辅助队列里的数据移动回数据队列。

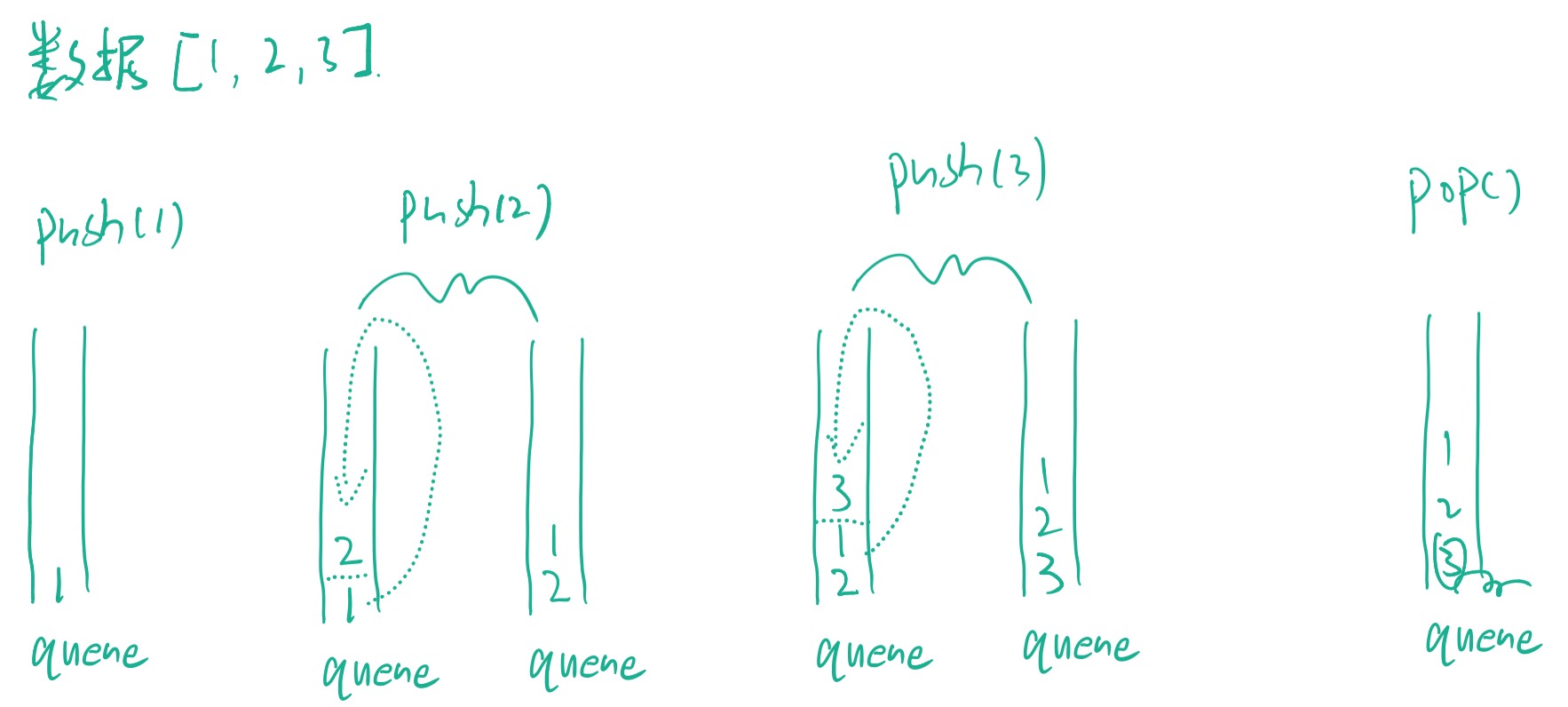
但是，仔细观察整个过程可以发现，只需要一个队列就可以实现。首先将新元素入队，并且假设新元素所在位置为n。然后将前n-1个元素出队再入队。

画图如下：

class MyStack:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.l1 = collections.deque()


    def push(self, x: int) -> None:
        """
        Push element x onto stack.
        """
        n = len(self.l1)
        # 将新元素入队
        self.l1.append(x)
        # 将前n-1个元素出队再入队
        for _ in range(n):
            self.l1.append(self.l1.popleft())


    def pop(self) -> int:
        """
        Removes the element on top of the stack and returns that element.
        """
        return self.l1.popleft()


    def top(self) -> int:
        """
        Get the top element.
        """
        return self.l1[0]


    def empty(self) -> bool:
        """
        Returns whether the stack is empty.
        """
        return not self.l1

复杂度分析：

时间复杂度：入栈O(n)，出栈O(1)，取栈顶元素O(1)，判空O(1)。

空间复杂度：入栈O(n)，出栈O(1)，取栈顶元素O(1)，判空O(1)。

---

最小值栈（简单）

为了能在常数时间内检索到栈内的最小元素，我们需要借助另外一个辅助栈来存储每次栈操作（push、pop、peek）后的最小值。

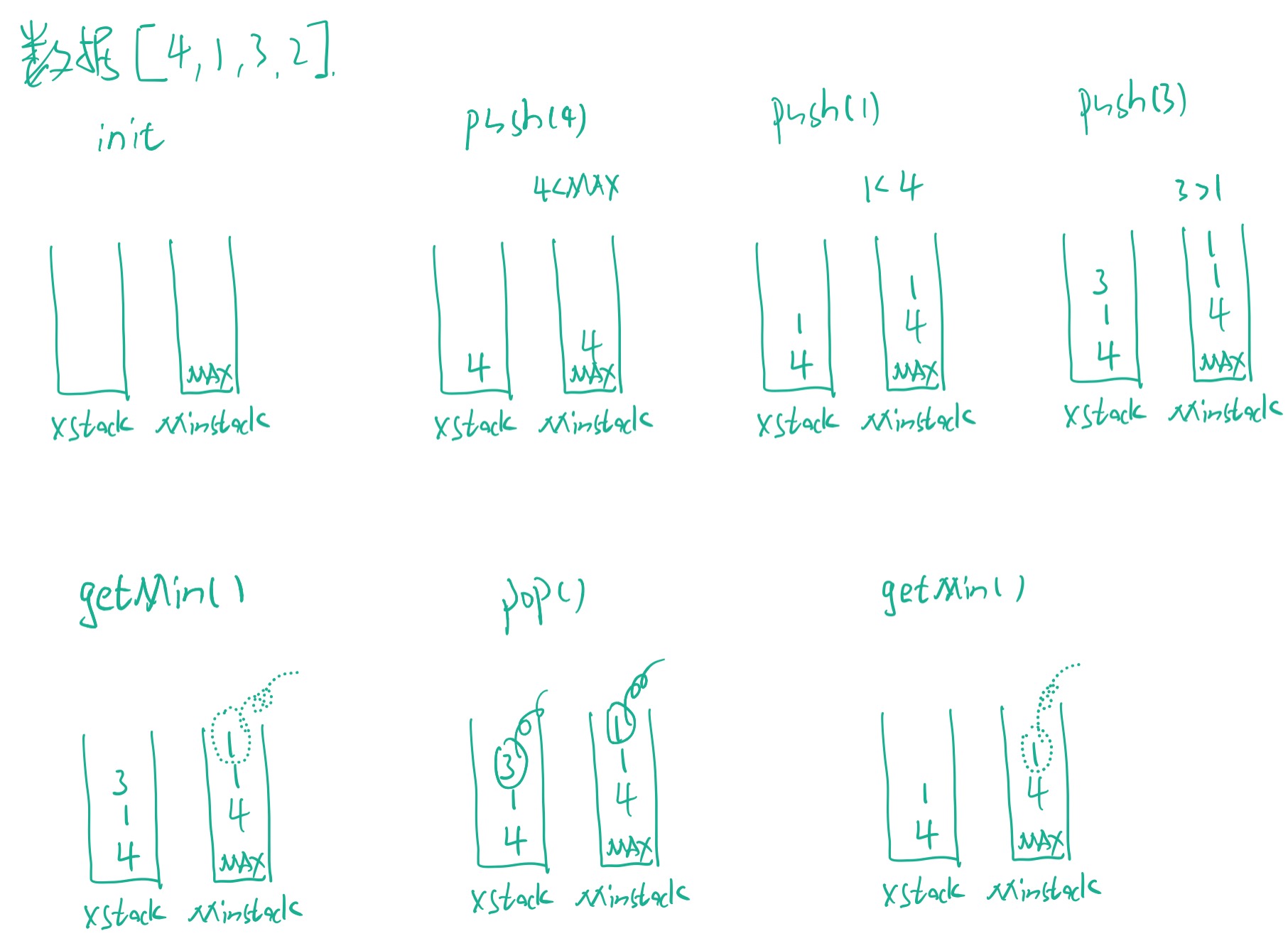
每次入栈都要检查辅助栈的栈顶元素和新入栈的元素谁更小，然后将小值入辅助栈。出栈只需要将两个栈同时出栈一个元素即可。

画图如下：

class MinStack {

    Deque<Integer> xStack;
    Deque<Integer> minStack;

    /** initialize your data structure here. */
    public MinStack() {
        xStack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        minStack.push(Integer.MAX_VALUE);
    }

    public void push(int x) {
        xStack.push(x);
        minStack.push(Math.min(minStack.peek(), x));
    }

    public void pop() {
        xStack.pop();
        minStack.pop();
    }

    public int top() {
        return xStack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

复杂度分析：

时间复杂度：O(1)，每个操作最多调用两次栈操作。

空间复杂度：O(n)。

---

用栈实现括号匹配（简单）

可以借助栈的先进后出特性来解此题。

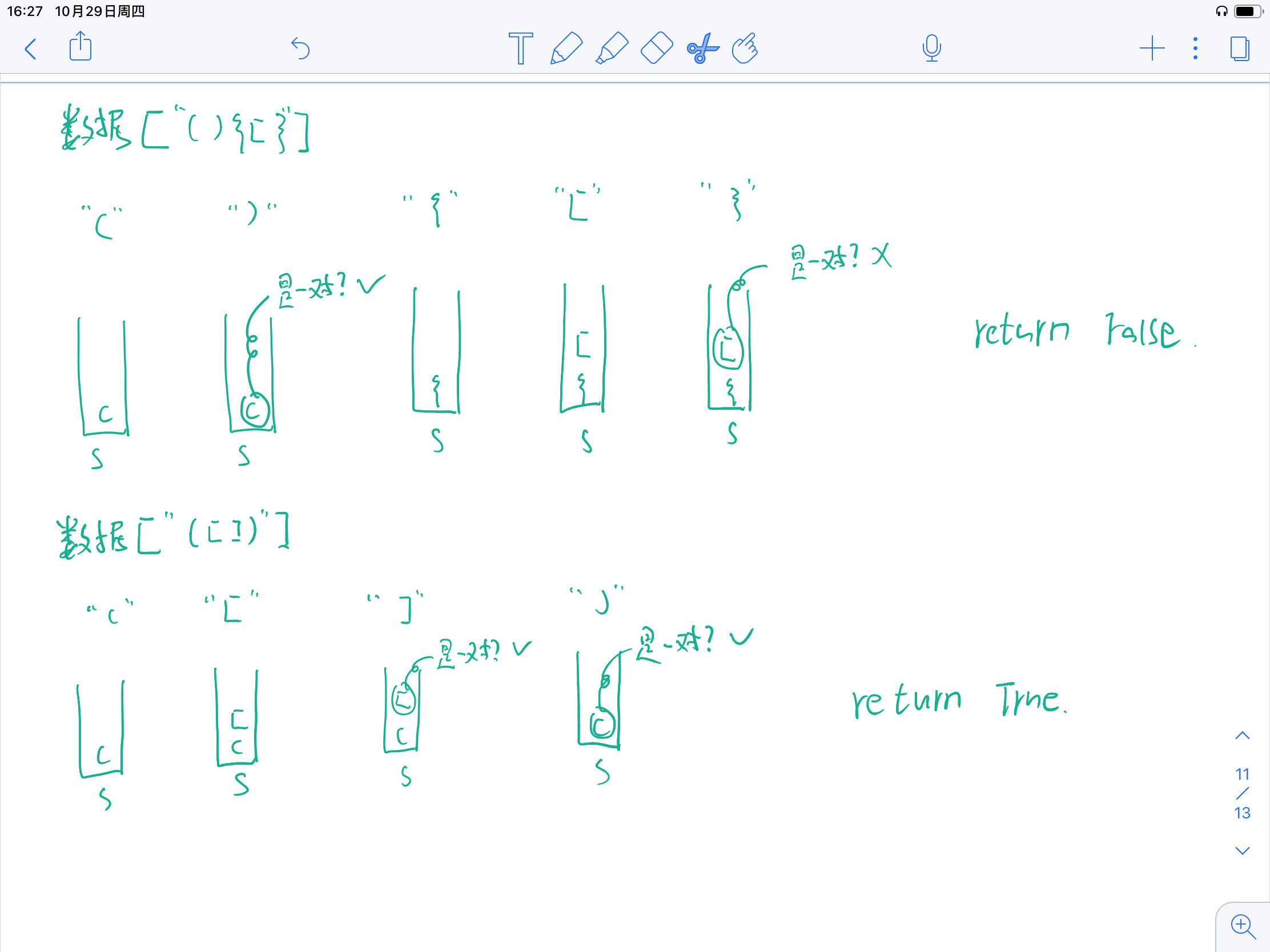
只要是左括号就入栈，如果是右括号则出栈一个元素，并且判断两者是否是一对，如果是一对，则继续处理下一个字符，否则括号不匹配return false。处理完所有括号以后，如果栈不空，则说明还有左括号没有配对return false。否则return true。

画图如下：

class Solution {
    public boolean isValid(String s) {
        Stack <Character> stack = new Stack<Character>();
        for(char c : s.toCharArray()) {
            if (c == '(' || c == '{' || c == '[') {
                stack.push(c);
            } else {
                if(stack.isEmpty()) {
                    return false;
                }
                char cTop = stack.pop();
                boolean r1 = c == ')' && cTop != '(';
                boolean r2 = c == '}' && cTop != '{';
                boolean r3 = c == ']' && cTop != '[';

                if(r1 || r2 || r3) {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

复杂度分析：

时间复杂度：O(n)。

空间复杂度：O(n)。

---

数组中元素与下一个比它大的元素之间的距离（中等）

这题可以用「单调栈」求解。所谓单调栈就是，通过一些巧妙地处理，使每次入栈操作后栈内元素都保持有序（单调递增、递减的）。单调栈通常用来处理Next Greater Element问题。

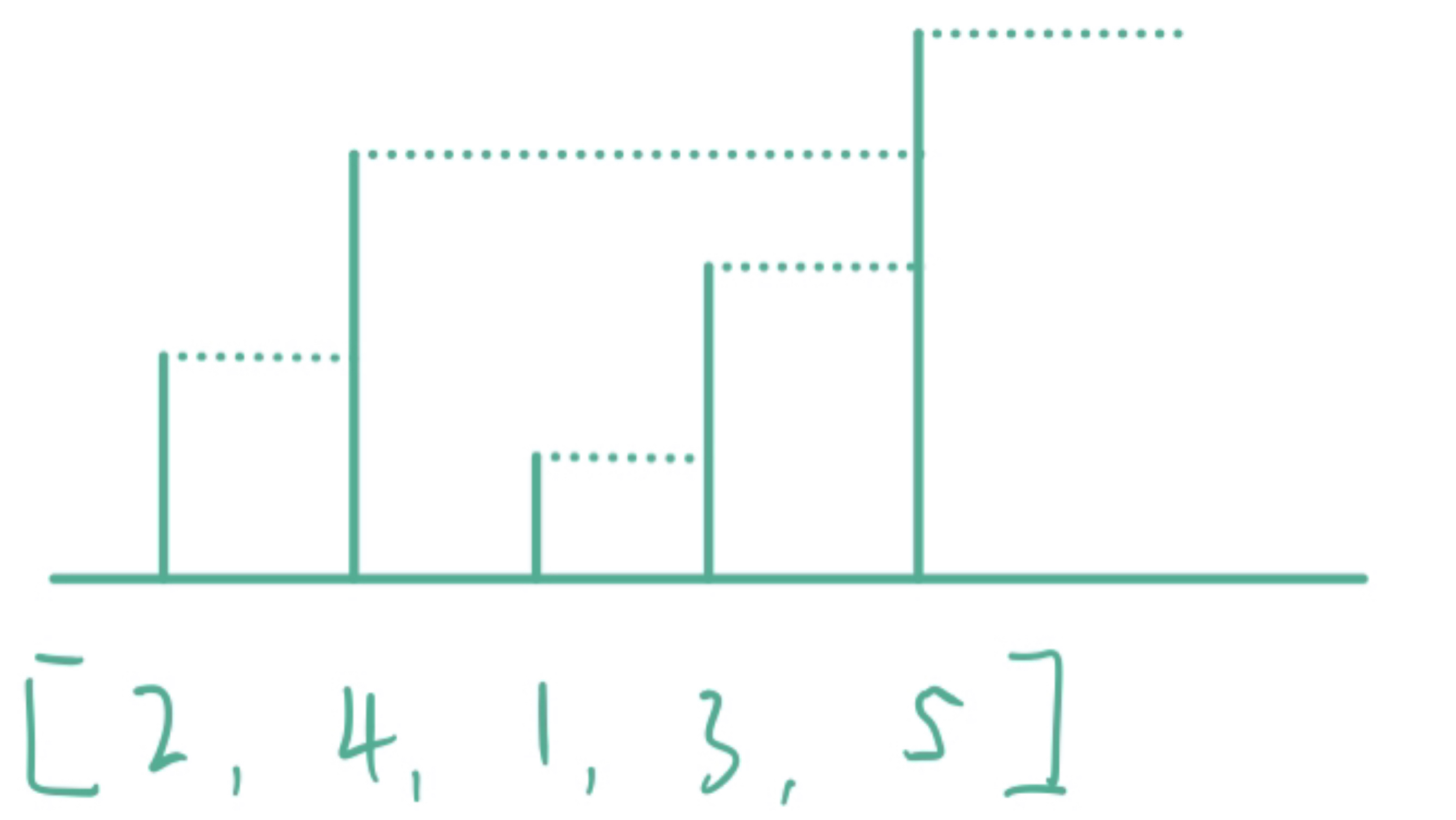
假设数据为[2, 4, 1, 3, 5]。我们可以将这组数据想象成五个不同身高的人并列站立，他们的身高分别为2，4，1，3，5。如下图：

矮个子右边第一个高个子会挡住矮个子的视线。我们现在想求2的Next Greater Element，该怎么办呢？只需要看2右边谁第一个个子比他高那就是谁。显然第一个高个子是4。所以2的Next Greater Element就是4。同理，4的Next Greater Element就是5。

class Solution {
    public int[] nextGreaterElement(int[] T) {
        Stack<Integer> s = new Stack<>();
        int[] ret = new int[T.length];
        for (int i = T.length - 1; i >= 0; -- i) {
            while (!s.isEmpty() && s.peek() <= T[i]) {
                s.pop();
            }
            ret[i] = s.isEmpty() ? -1 : s.peek();
            s.push(T[i]);
        }
        return ret;
    }
}

别急接着往下看。

为了提高代码执行效率，我们应该「从右往左」处理数据，这好像有点「预测未来」的感觉，就是提前知道了谁比你高，不用去一个个的和下一个比。

代码中我们借助了栈这种先进后出的数据结构。并且将数据倒着入栈。while循环可以帮助我们将两个高个子之间的矮个子排除掉。通过这些可以保证栈里的数据按照「高个在下，矮个在上」排序。

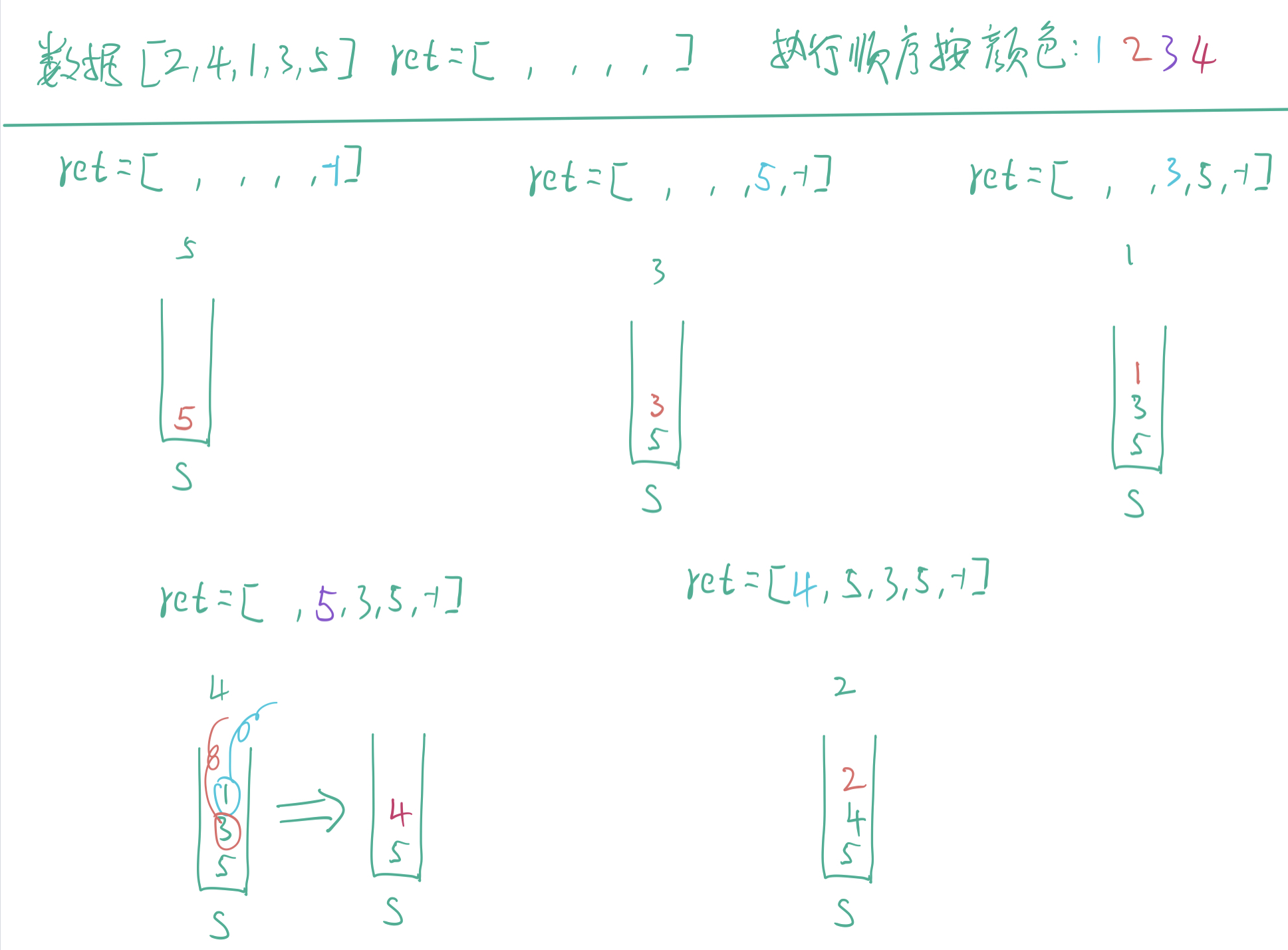
画图如下:

可以按照上图一步一步的走一遍，加深理解。

对于本题，思路和上面一样，就是入栈的不是数值，而是下标，这点要注意区分。

class Solution {
    public int[] dailyTemperatures(int[] T) {
        Stack<Integer> s = new Stack<>();
        int[] ret = new int[T.length];
        for (int i = T.length - 1; i >= 0; -- i) {
            while (!s.isEmpty() && T[s.peek()] <= T[i]) {
                s.pop();
            }
            ret[i] = s.isEmpty() ? 0 : s.peek() - i;
            s.push(i);
        }
        return ret;
    }
}

复杂度分析：

时间复杂度：O(n)。不要看到这里有嵌套循环就觉得应该是O(n^2)的复杂度。其实对于内层的while循环，最多执行数组长度遍，每个元素入栈一次，但是出栈最多一次。

空间复杂度：O(n)。

---

循环数组中比当前元素大的下一个元素（中等）

这题大概的思路还是用单调栈来处理，但是对于循环数组，该怎么处理呢？比如对于循环数组[1, 2, 1]，末尾的1通过绕一圈才找到Next Greater Element2。

对于这题，可以想到将数组长度翻倍变为[1, 2, 1, 1, 2, 1]，然后直接套用上题解法得到结果数组ret=[2, -1, 2, 2, -1, -1]然后取前3位即可。

然而一般我们对于循环数组，可以用「取余」操作来处理循环，从而模拟了数组长度翻倍的效果。

---

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int l = nums.length;
        int[] ret = new int[l];
        Stack<Integer> s = new Stack<>();
        for ( int i = 2 * l - 1; i >= 0; -- i) {
            while (!s.isEmpty() && s.peek() <= nums[i % l]) {
                s.pop();
            }
            ret[i % l] = s.isEmpty() ? -1 : s.peek();
            s.push(nums[i % l]);
        }
        return ret;
    }
}

复杂度分析：

时间复杂度：O(n)。

空间复杂度：O(n)。